To access material, start machines and answer questions login.
Introduction
Cryptography is designed to protect sensitive data, but it's only effective when implemented correctly. Even small mistakes in how cryptographic systems are set up can open the door for attackers. These mistakes are surprisingly common and often become "quick wins" during penetration testing or real-world attacks.
For example, using a weak encryption key or a predictable random number generator can make encryption easier to break. Similarly, exposing secrets like API keys in client-side code gives attackers everything they need to bypass cryptographic protections. The key takeaway here is that it's not always the algorithm itself that's flawed—it's how it's used.
Objectives
By the end of this room, you will:
- Understand why cryptographic mistakes occur and their impact on security.
- Recognise and exploit vulnerabilities like weak encryption keys and poorly configured algorithms.
- Learn how to identify and exploit issues like exposed keys.
- Understand how to secure cryptographic systems by avoiding these mistakes.
Prerequisites
Before starting this room, you should have a basic understanding of the following concepts:
- How cryptographic concepts like encryption, decryption, and hashing work.
- Tools like Hashcat or John the Ripper are used to crack passwords and keys.
- HTTP request and response basics, along with some experience using the command line.
- Completion of Cryptography and Cryptography-101 modules.
Starting the Machine
Deploy the target VM attached to this task by pressing the green Start Machine button. After obtaining the machine's generated IP address, you can either use the AttackBox or your own VM connected to TryHackMe's VPN.
You can access the web app by visiting the URL http://bcts.thm/ but first, you must add the hostname in your OS or AttackBox.
How to add hostname (click to read)
- If you are connected via VPN or the AttackBox, you can add the hostname
bcts.thmby first opening the host file, depending on your host operating system. - Windows:
C:\Windows\System32\drivers\etc\hosts - Ubuntu or AttackBox:
/etc/hosts - Open the host file and add a new line at the end of the file in the format:
MACHINE_IP bcts.thm - Save the file and type
http://bcts.thm/in the browser to access the website.
We will be using the web application running on this machine in the upcoming tasks.
I have started the target machine and I'm ready to break crypto!
Cryptography relies on the premise that keys used in encryption are computationally infeasible to guess. A "strong" key is one that provides a high level of entropy (unpredictability) and sufficient length to make brute-force attacks impractical. For example, a 128-bit key has 2^128 possible combinations, which would take centuries to brute-force using modern hardware.
Characteristics of Strong Keys:
- Length: Longer keys significantly increase the computational effort required to brute-force them.
- Entropy: Keys must be truly random, not derived from predictable inputs like timestamps or user data.
- Uniqueness: Keys must be unique across different encryptions or systems to prevent correlation attacks.
When these principles are violated, keys become vulnerable to brute-force or mathematical attacks.
Math of RSA
RSA encryption, named after its inventors Rivest, Shamir, and Adleman, is based on the difficulty of factoring large numbers.
A public key consists of:
- n=p×q: The product of two large prime numbers, (p) and (q).
- e: A small public exponent (commonly (e = 65537)).
The private key is derived from:
- ϕ(n)=(p−1)×(q−1), where ϕ is Euler's totient function.
- (d): The modular inverse of 𝑒 e modulo 𝜙 ( 𝑛 ) ϕ(n), satisfying 𝑒 × 𝑑 ≡ 1 ( mod 𝜙 ( 𝑛 ) ) e×d≡1 (mod ϕ(n)).
The security of RSA depends on the difficulty of factoring (n) into its prime components (p) and (q). However, if (p) or (q) is poorly generated or shared across keys, this foundational assumption breaks down.
How Factorisation Time Increases Exponentially
To demonstrate how factoring time grows with larger primes, we will test factorisation for different values of (n = p * q) using Python.
import time
from sympy.ntheory import factorint
# Small n (product of two small primes)
n_small = 253 # 11 × 23
start = time.time()
factorint(n_small)
print(f"Time to factor {n_small}: {time.time() - start:.6f} seconds")
# Medium n
n_medium = 988027 # 941 × 1051
start = time.time()
factorint(n_medium)
print(f"Time to factor {n_medium}: {time.time() - start:.6f} seconds")
# Large n
n_large = 2147483647 # A large prime
start = time.time()
factorint(n_large)
print(f"Time to factor {n_large}: {time.time() - start:.6f} seconds")The above script will have an output of:
Time to factor 253: 0.000019 seconds
Time to factor 988027: 0.000041 seconds
Time to factor 2147483647: 0.000094 secondsAs prime numbers grow larger, factorisation time increases exponentially, making brute-force factorisation infeasible for properly generated RSA keys.
What is "P's and Q's"?
The paper "P's and Q's" by Ross Anderson and Serge Vaudenay explores how poor randomness in RSA key generation can lead to severe vulnerabilities. It outlines key weaknesses that attackers can exploit:
Predictable Primes:
If (p) or (q) are generated using a weak random number generator (e.g., seeded with system time), an attacker can recreate the key generation process and derive the primes.
Shared Primes Across Keys:
When multiple RSA keys share a common prime (p), the attacker can use the greatest common divisor (GCD) method to factor n1=p×q1 and n2=p×q2, breaking both keys.
Small Differences Between Primes:
If (p) and (q) are too close in value, efficient algorithms such as Fermat's factorisation method can quickly factor (n).
Mathematical Exploits Using GCD:
The GCD of two public keys that share a prime can be computed in polynomial time:
GCD(n1,n2)=p
These vulnerabilities highlight the critical importance of randomness and diversity in prime generation for RSA security.
Exercise
Note: Remember to include all values and required imports. The factoring step is not required in the script.
Using the c, n, and e, which are crucial components of the RSA encryption process. The RSA algorithm also utilises two large prime numbers, p and q. Can you uncover the hidden text behind it? Follow along to build a script that will uncover the hidden text.
Public Key: n = 43941819371451617899582143885098799360907134939870946637129466519309346255747
Exponent: e = 65537
Ciphertext: c = 9002431156311360251224219512084136121048022631163334079215596223698721862766Your task is to recover the plaintext by factoring n and deriving the private key. The challenge assumes n is a product of two weakly generated primes p and q.
Factoring
Since (n) is the product of two large primes ((p) and (q)), factorisation is the first step. Modern factoring tools, like MSIEVE or YAFU, can be used for this purpose. However, for educational purposes, you can use Python and a library like sympy.
Use the following Python code to factor (n) into (p) and (q):
Note: This computation takes a lot of processing power, so if you are using the AttackBox, we strongly recommend that you skip this step and follow along.
from sympy import factorint
from Crypto.Util.number import inverse, long_to_bytes
# Given values
n = 43941819371451617899582143885098799360907134939870946637129466519309346255747
# Factor n
factors = factorint(n)
p, q = factors.keys()
print("Prime factors:")
print("p =", p)
print("q =", q)Expected Output:
The script will compute:
p = 205237461XXXXXXXXXXXXX
q = 21410233XXXXXXXXXXXXXX Alternatively, you can use FactorDB and search for the prime numbers of the (n). For example:

Compute phi
Using the two primes, calculate phi(n), where:
phi_n = (p - 1) * (q - 1)
print("Phi(n) =", phi_n)Finding the Private Key
The private key exponent (d) is the modular inverse of (e) modulo (ϕ(n)):
Use Python to calculate (d):
from sympy import factorint
from Crypto.Util.number import inverse, long_to_bytes
e = 65537
d = inverse(e, phi_n)
print("Private key (d):", d)Decrypting the Ciphertext
Now that you have (d), decrypt the given ciphertext (c):
Use Python to compute the plaintext:
c = 9002431156311360251224219512084136121048022631163334079215596223698721862766
plaintext = pow(c, d, n)
flag = long_to_bytes(plaintext)
print(flag.decode())
print("Decrypted Plaintext:", flag)Key Takeaways from Broadcast RSA
- Avoid small public exponents like
e = 3; instead, use larger values likee = 65537. - Ensure encrypted messages are padded with random data (e.g., PKCS#1 or OAEP) to prevent mathematical attacks.
- Use different plaintexts for different recipients to avoid the conditions that make CRT attacks possible.
What is the flag?
Hashing is a cryptographic process that transforms an input (e.g., a password or a message) into a fixed-size string, often called a hash. The transformation is one-way, meaning it’s not feasible to reverse the hash to recover the original input. Hashing is used for:
- Password Storage: Instead of storing plaintext passwords, systems store their hashes. During login, the input password is hashed and compared to the stored hash.
- Data Integrity: Hashes verify that data has not been altered during transmission.
- Message Authentication (HMAC): Hashes combined with a secret key verify that a message hasn’t been tampered with.
Common Vulnerabilities in Hashing
Weak Hash Algorithms
Older algorithms like MD5 and SHA-1 are considered insecure due to their susceptibility to collisions (two inputs producing the same hash). Attackers can exploit this to craft malicious data with the same hash.
Lack of Salting
When the same input consistently produces the same hash, attackers can use precomputed databases (rainbow tables) to reverse the hash to its original value. Salting—adding a unique, random value to each input before hashing—prevents this.
Insecure HMACs
Hash-based Message Authentication Codes (HMACs) rely on a hash function combined with a secret key to ensure message authenticity. Weaknesses arise when:
- The hash function is insecure.
- The key is short, predictable, or reused.
SHA-256 Isn’t Ideal for Password Hashing
SHA-256 is a widely used cryptographic hash function, particularly for verifying data integrity in digital signatures and file verification. It’s designed to be fast and efficient, which is perfect for those applications. However, when it comes to password hashing, speed is the enemy.
Attackers rely on brute-force and dictionary attacks to guess passwords. The faster a hash function runs, the faster it can test password guesses. SHA-256, like MD5 and SHA-1, is optimised for speed, making it a poor choice for password storage.
On modern GPUs, attackers can compute billions of SHA-256 hashes per second, making brute-force attacks highly effective. This is why Password Hashing Schemes (PHS) like Argon2, bcrypt, and PBKDF2 exist. These functions are specifically designed to be computationally expensive, slowing down brute-force attacks.
One of the key advantages of password hashing schemes is adaptability. SHA-256 takes a fixed amount of time to compute a hash, but bcrypt and Argon2 allow developers to adjust their "cost" parameters. This means that as computing power increases, the functions can be reconfigured to stay slow, keeping attacks impractical.
To put this into perspective, here’s a rough comparison of how many hashes per second different algorithms can process using GPU acceleration:
| Hash Function | Hashes per Second (Approximate, GPU-accelerated) |
|---|---|
| MD5 | ~100 billion H/s |
| SHA-256 | ~1 billion H/s |
| bcrypt (cost=12) | ~1000 H/s |
| Argon2id | ~100 H/s |
If an attacker is trying to brute-force a password, SHA-256 allows them to test billions of possibilities per second, while bcrypt and Argon2 intentionally slow them down to just a few thousand or even hundreds per second. This makes an enormous difference in security.
While SHA-256 can be used for password hashing if you add a salt and manually iterate the hashing process many times, this is still a weaker approach than using a proper password hashing function. Argon2, bcrypt, and PBKDF2 include built-in protections against brute-force attacks, making them far better suited for storing passwords securely.
Choosing the Right Hashing Function
To clarify when to use different hash functions, here’s a comparison:
| Purpose | Recommended Hashing Method | Why? |
|---|---|---|
| Storing Passwords | Argon2, bcrypt, PBKDF2 | Designed to be slow and adaptive, making brute-force attacks impractical. |
| Data Integrity (Checksums, File Verification) | SHA-256, SHA-3, BLAKE2 | Fast and efficient, but unsuitable for password security. |
| Message Authentication (HMAC) | HMAC-SHA256, HMAC-SHA3 | Used to verify message integrity, not for storing passwords. |
Using SHA-256 for password hashing doesn’t immediately expose passwords, but it does make brute-force attacks far more effective than they would be with a proper password hashing scheme.
For general cryptographic purposes, SHA-256 is excellent. It’s used in digital signatures, message authentication codes (HMAC), and file integrity verification because speed is an advantage in those cases. But for password storage, it should not be used. Instead, the correct approach is to use Argon2, bcrypt, or PBKDF2, all of which make brute-force attacks impractical by design.
Many developers assume that hashing alone is enough to secure passwords, but the reality is that the right tool needs to be used for the right job. Using SHA-256 to hash passwords is like using a padlock on a bank vault—it provides some protection, but it’s not nearly strong enough to stop a determined attacker.
Challenge
HMAC (Hash-based Message Authentication Code) is a cryptographic method used to verify the integrity and authenticity of a message. It combines a cryptographic hash function (in this case, SHA-1) with a secret key. If an attacker can determine the secret key, they can forge valid HMACs and manipulate messages.
In this challenge, you are given a message along with its HMAC-SHA1 digest. However, the secret key used for signing is weak. Your objective is to recover the key.
Below is the message and the SHA1 digest of that message.
Message: CanYouGuessMySecret
SHA1-Digest: 1484c3a5d65a55d70984b4d10b1884bda8876c1dSolution
Hashcat is a powerful tool for cracking hashes and HMAC keys. Since we know the format is HMAC-SHA1 , we will use mode 150 . Mode 150 targets HMAC-SHA1 based on this documentation.
Save the hash and message into a file:
echo -n "1484c3a5d65a55d70984b4d10b1884bda8876c1d:CanYouGuessMySecret" > digest.txtRun Hashcat with the RockYou wordlist:
hashcat -a 0 -m 150 digest.txt /usr/share/wordlists/rockyou.txtBelow is the expected output:
user@tryhackme $ hashcat -a 0 -m 150 digest.txt /usr/share/wordlists/rockyou.txt
hashcat (v6.2.6) starting
OpenCL API (OpenCL 3.0 PoCL 6.0+debian Linux, None+Asserts, RELOC, LLVM 17.0.6, SLEEF, POCL_DEBUG) - Platform #1 [The pocl project]
====================================================================================================================================
* Device #1: cpu--0x000, 1436/2937 MB (512 MB allocatable), 4MCU
Minimum password length supported by kernel: 0
Maximum password length supported by kernel: 256
Hashes: 1 digests; 1 unique digests, 1 unique salts
Bitmaps: 16 bits, 65536 entries, 0x0000ffff mask, 262144 bytes, 5/13 rotates
Rules: 1
Optimizers applied:
* Zero-Byte
* Not-Iterated
* Single-Hash
* Single-Salt
ATTENTION! Pure (unoptimized) backend kernels selected.
Pure kernels can crack longer passwords, but drastically reduce performance.
If you want to switch to optimized kernels, append -O to your commandline.
See the above message to find out about the exact limits.
Watchdog: Temperature abort trigger set to 90c
Host memory required for this attack: 0 MB
Dictionary cache hit:
* Filename..: /usr/share/wordlists/rockyou.txt
* Passwords.: 14344385
* Bytes.....: 139921507
* Keyspace..: 14344385
1484c3a5d65a55d70984b4d10b1884bda8876c1d:CanYouGuessMySecret:xxxxxxxxx
Session..........: hashcat
Status...........: Cracked
Hash.Mode........: 150 (HMAC-SHA1 (key = $pass))
Hash.Target......: 1484c3a5d65a55d70984b4d10b1884bda8876c1d:CanYouGues...Secret
Time.Started.....: Tue Feb 4 19:58:08 2025 (0 secs)
Time.Estimated...: Tue Feb 4 19:58:08 2025 (0 secs)
Kernel.Feature...: Pure Kernel
Guess.Base.......: File (/usr/share/wordlists/rockyou.txt)
Guess.Queue......: 1/1 (100.00%)
Speed.#1.........: 1209.9 kH/s (0.27ms) @ Accel:256 Loops:1 Thr:1 Vec:4
Recovered........: 1/1 (100.00%) Digests (total), 1/1 (100.00%) Digests (new)
Progress.........: 1024/14344385 (0.01%)
Rejected.........: 0/1024 (0.00%)
Restore.Point....: 0/14344385 (0.00%)
Restore.Sub.#1...: Salt:0 Amplifier:0-1 Iteration:0-1
Candidate.Engine.: Device Generator
Candidates.#1....: 123456 -> bethany
Hardware.Mon.#1..: Util: 43%
Started: Tue Feb 4 19:58:07 2025
Stopped: Tue Feb 4 19:58:10 2025
What is the secret used to encrypt the message?
Risks of Exposing Cryptographic Keys in Client-Side Code
Exposing cryptographic keys in client-side code is a common yet critical mistake. When keys are included in code that runs in the user's browser (e.g., JavaScript), anyone with access to the application can retrieve and misuse those keys. This defeats the purpose of encryption and authentication, as the attacker gains direct access to the mechanism meant to protect the data.
Key risks include:
- Unauthorised Access: Exposed keys can be used to decrypt sensitive data or interact with backend APIs as an authenticated user.
- Data Tampering: An attacker can use the keys to generate signed payloads or modify encrypted messages, bypassing integrity checks.
- API Abuse: Hardcoded API keys may allow attackers to access privileged API endpoints without authorisation.
Common Scenarios of Key Exposure
- Hardcoded API Keys in JavaScript
Developers often embed API keys in front-end code for convenience, forgetting that anyone can view this code using browser developer tools. - Encryption Keys in Client-Side Frameworks
Encryption keys are sometimes included in front-end libraries or scripts to encrypt/decrypt data locally. These keys can be easily extracted and used maliciously. - Unsecured Configuration Files
Configuration files embedded in web applications may contain sensitive credentials or keys in plain text.
Exercise
Navigate to http://bcts.thm/labs/lab3.
Open your developer tools (F12), navigate to the network tab, and try submitting a message.
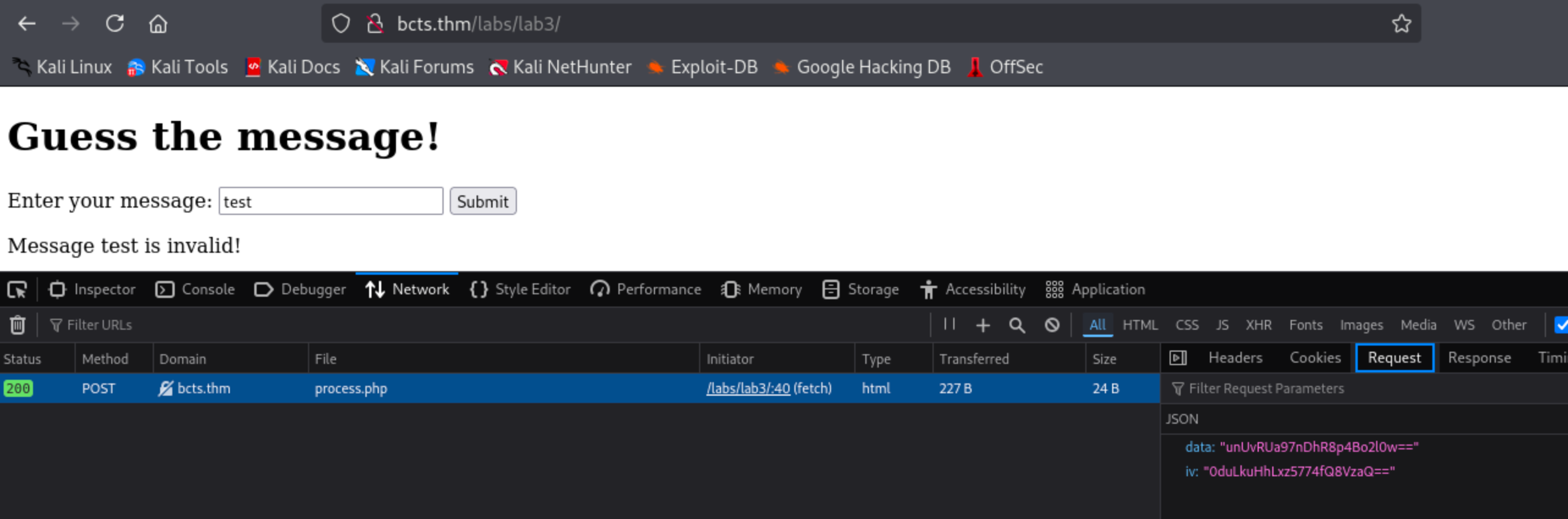
As you can see in the image above, the submitted data is encrypted using the data parameter as shown in the request. Checking the source code of the web page will show that the application uses JavaScript to encrypt the submitted message before submitting it to process.php.
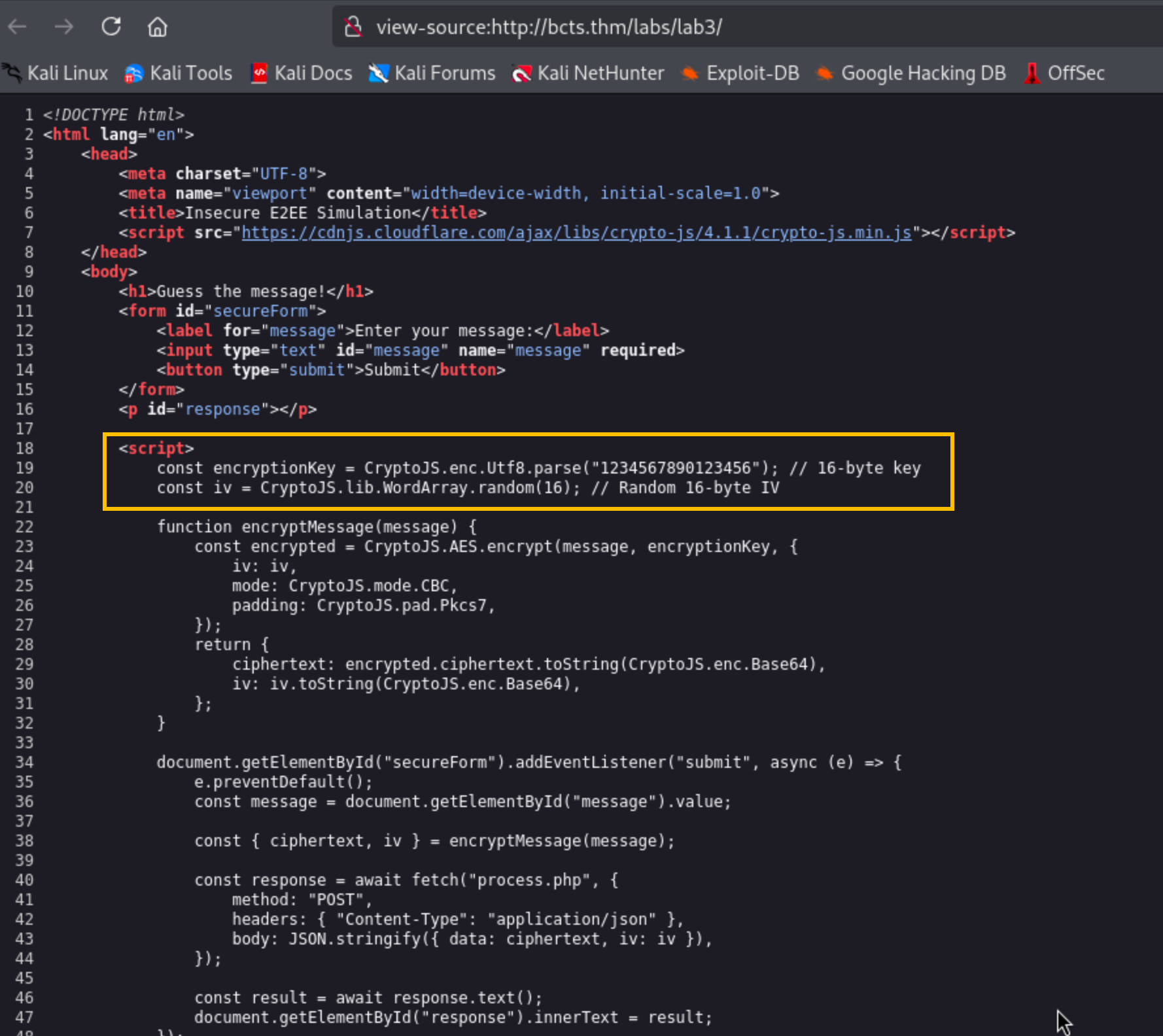
Since the encryption key used to encrypt the message is hardcoded in the JavaScript code, it is possible for an attacker to create a script that will brute force for the correct message using the hardcoded encryptionKey value.
To simplify this, a wordlist containing the possible message is available on the server at http://bcts.thm/labs/lab3/wordlist.txt.
However, directly brute-forcing the application will not work since the request is encrypted, so we must automate this using Python.
Below is the sample Python script that uses the available wordlist.txt in the server.
Note: If you're using your own machine, you must install pycryptodome using pip for the script to work.
import requests
import base64
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
# Configuration
url = "http://bcts.thm/labs/lab3/process.php"
encryption_key = b"1234567890123456" # Must be 16 bytes (same as in the JavaScript)
wordlist_path = "wordlist.txt" # Path to the wordlist
# Function to encrypt a message
def encrypt_message(message, iv):
# Pad the message to a multiple of the block size (16 bytes for AES)
padded_message = pad(message.encode(), AES.block_size)
# Encrypt using AES-CBC
cipher = AES.new(encryption_key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(padded_message)
# Encode ciphertext and IV in Base64 for transmission
return base64.b64encode(ciphertext).decode(), base64.b64encode(iv).decode()
# Function to send the payload
def send_payload(ciphertext, iv):
payload = {"data": ciphertext, "iv": iv}
response = requests.post(url, json=payload)
return response.text
# Main bruteforce function
def bruteforce():
with open(wordlist_path, "r") as f:
words = f.readlines()
for word in words:
word = word.strip()
print(f"Trying: {word}")
# Generate a random IV (16 bytes)
iv = AES.get_random_bytes(16)
# Encrypt the current word
ciphertext, iv_base64 = encrypt_message(word, iv)
# Send the payload to the server
response = send_payload(ciphertext, iv_base64)
print(f"Response: {response}")
# Check if the response indicates success
if "Access granted!" in response:
print(f"[+] Found the correct message: {word}")
break
if __name__ == "__main__":
bruteforce()
View Explanation
Script Setup
- url: The script interacts with
http://bcts.thm/labs/lab3/process.php, where the encrypted message is sent. - wordlist_path: The file containing potential plaintext words used for brute-forcing.
Encryption Key:
- encryption_key: The AES encryption key is hardcoded as
b"1234567890123456", which is the encryption key hardcoded in the JavaScript file of the application.
Functions
encrypt_message(message, iv):
- Encrypts a given message using AES-CBC mode.
- Pads the message to ensure its length is a multiple of the AES block size (16 bytes).
- Encrypts the padded message using AES with the provided IV.
- Converts the ciphertext and IV to Base64 format before returning.
send_payload(ciphertext, iv):
- Sends the encrypted message and IV as a JSON payload to the target server.
- Returns the server's response.
bruteforce():
- Reads the wordlist from
wordlist.txt. - Iterates over each word in the list:
- Generates a random IV (16 bytes).
- Encrypts the word using AES-CBC.
- Sends the encrypted message to the server.
- Check if the response contains
"Access granted!"(indicating success).
Response Handling:
- If the response contains
"Access granted!", the correct plaintext is found, and the script exits. - Otherwise, it proceeds to the next word in the list.
Once the script successfully brute forces the correct message, the application will return the flag.
Note: If you're using the AttackBox, use python3.9 instead of python3.
user@tryhackme$ $ python3 exploit.py
Trying: jadmxqtideg
Response: Message jadmxqtideg is invalid!
Trying: pyasosedg
Response: Message pyasosedg is invalid!
Trying: qdmicq
Response: Message qdmicq is invalid!
[--snip--]
Response: Access granted! Here's your flag: THM{XXXXXXXXXXXXXXXXXXXXXXX}
[+] Found the correct message: XXXXXXXXXXX
Key Takeaways
- Never Hardcode Keys: Avoid embedding sensitive keys in client-side code or configuration files that are accessible to users.
- Use Secure Key Management: Store keys in secure environments, such as server-side applications or dedicated key management services (e.g., AWS KMS, Azure Key Vault).
- Implement Backend Encryption: Perform sensitive operations, like encryption and decryption, on the server side to prevent exposure of critical secrets.
- Educate Developers: Many developers make this mistake unknowingly. Awareness and secure coding practices can prevent these vulnerabilities.
By exploiting a hardcoded encryption key, you've seen how this simple mistake can expose an application's sensitive data to attackers.
What is the flag?
What is Unauthenticated Encryption?
Unauthenticated encryption refers to encryption that does not include a mechanism to verify the integrity or authenticity of the ciphertext. This means that an attacker can modify encrypted data that is in transit, and the system will still accept and process it without detecting any tampering.
When the application decrypts tampered ciphertext without verifying its integrity, an attacker can manipulate the plaintext in predictable ways. This is the root cause of bit-flipping attacks.
A classic example is AES in CBC (Cipher Block Chaining) mode without an authentication tag. AES-CBC encrypts data securely but does not ensure integrity. If an attacker can modify the ciphertext, they can manipulate certain bits of the decrypted plaintext without breaking the encryption.
This leads to bit-flipping attacks, where an attacker changes ciphertext in a way that results in controlled modifications in the plaintext.
Bit Flipping Attacks
Bit flipping attacks target systems that use unauthenticated encryption, allowing an attacker to modify ciphertext so that the decrypted plaintext is manipulated in predictable ways. This type of attack is particularly dangerous when systems assume that encrypted data is inherently safe to trust without verifying its integrity.
Encryption schemes like AES-CBC (Cipher Block Chaining) are vulnerable to bit flipping when no integrity check, such as a Message Authentication Code (MAC), is applied. In CBC mode:
- The plaintext is XORed with the previous ciphertext block before encryption.
- If an attacker alters bits in a ciphertext block, it changes the corresponding plaintext block during decryption.
For example, consider an encrypted payload:
{"role":"0"}If this ciphertext is tampered with, the role could be escalated to "1". Without integrity protection, the system would accept the manipulated plaintext as legitimate.
Exercise
Navigate to http://bcts.thm/labs/lab4/.
The application accepts any credential as shown below:
if ($_SERVER['REQUEST_METHOD'] === 'POST' && isset($_POST['username'], $_POST['password'])) {
$username = htmlspecialchars($_POST['username']);
$password = htmlspecialchars($_POST['password']);
$message = "username={$username}";
$role = "0";
$token = encrypt_data($message, $key, $iv);
$token2 = encrypt_data($role, $key, $iv);
setcookie("auth_token", $token, time() + 3600, "/");
setcookie("role", $token2, time() + 3600, "/");
header("Location: dashboard.php");
exit();
}
As we can see in the code above, the cookie named role uses an encrypted version of the text 0.
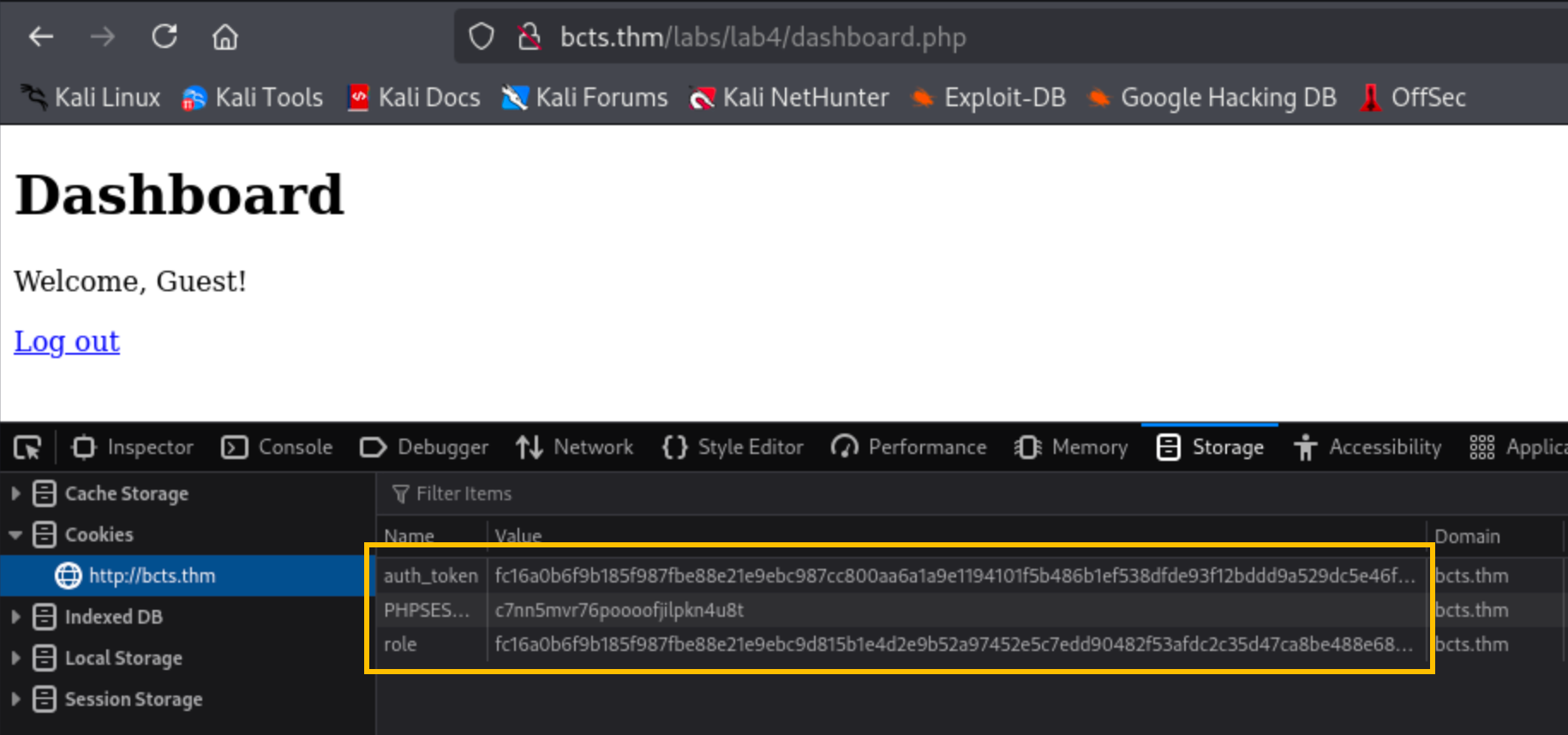
Below is a sample script that will flip the role=0 to role=1.
import base64, sys
from binascii import unhexlify, hexlify
original_token = sys.argv[1] # Your encrypted role token goes here
try:
cipher_bytes = bytearray(unhexlify(original_token))
except ValueError:
print("Invalid token format! Make sure it's a valid hex string.")
exit(1)
# AES block size
block_size = 16
# Debug: Print IV (first 16 bytes) before modification
print("\n[DEBUG] Original IV (First 16 Bytes):", hexlify(cipher_bytes[:block_size]).decode())
guest_offset = 0
xor_diff = [
0x01, # '0' -> '1'
]
# Apply bit flipping to the IV (first 16 bytes)
for i, diff in enumerate(xor_diff):
print(f"[DEBUG] Modifying byte at offset {guest_offset + i}: {hex(cipher_bytes[guest_offset + i])} XOR {hex(diff)}")
cipher_bytes[guest_offset + i] ^= diff
print("\n[DEBUG] Modified IV (First 16 Bytes):", hexlify(cipher_bytes[:block_size]).decode())
# Encode the modified token back to hex
modified_token = hexlify(cipher_bytes).decode()
print("\nModified Token:")
print(modified_token)
print("\nUse this token as the new 'role' cookie in your browser to log in as admin.")
Click here for a breakdown of the script.
original_token:
original_token = "" # Put your encrypted role token here
- This should contain the AES-encrypted role token located in the cookies tab of your browser.
Hex Decoding:
try:
cipher_bytes = bytearray(unhexlify(original_token))
except ValueError:
print("Invalid token format! Make sure it's a valid hex string.")
exit(1)
- Converts the hex-encoded token into a bytearray for modification.
- If the token is not in a valid hex format, an error is printed, and the script exits.
AES Block Size and Initialization Vector (IV)
block_size = 16
- AES uses a 16-byte block size.
- The first 16 bytes of the encrypted token represent the IV in AES-CBC mode.
Debugging: Print the Original IV
print("\n[DEBUG] Original IV (First 16 Bytes):", hexlify(cipher_bytes[:block_size]).decode())
- The script prints the IV before modification to track changes.
Bit-Flipping Attack
guest_offset = 0
xor_diff = [
0x01, # '0' -> '1'
]
- Bit-flipping works by modifying the IV to change the decrypted plaintext.
- guest_offset = 0 means the modification starts at byte 0 of the IV.
- The script applies an XOR operation (
^=) to change a specific byte in the IV.- In this case, it changes '0' to '1' in the decrypted text.
Applying the Bit Flip
for i, diff in enumerate(xor_diff):
print(f"[DEBUG] Modifying byte at offset {guest_offset + i}: {hex(cipher_bytes[guest_offset + i])} XOR {hex(diff)}")
cipher_bytes[guest_offset + i] ^= diff
- Iterates over
xor_diffand modifies the corresponding bytes in the IV. - Uses XOR (
^=) to modify the first byte of the IV.
Debugging: Print the Modified IV
print("\n[DEBUG] Modified IV (First 16 Bytes):", hexlify(cipher_bytes[:block_size]).decode())
- Prints the new IV after modification.
Encoding
modified_token = hexlify(cipher_bytes).decode()
print("\nModified Token:")
print(modified_token)
print("\nUse this token as the new 'role' cookie in your browser to log in as admin.")
- Converts the modified token back into a hex-encoded string.
Run the script above.
user@tryhackme$ $ python3 exploit.py 41a27XXXXXXXXXX
[DEBUG] Original IV (First 16 Bytes): fc16a0b6f9b185f987fbe88e21e9ebc9
[DEBUG] Modifying byte at offset 0: 0xfc XOR 0x1
[DEBUG] Modified IV (First 16 Bytes): fd16a0b6f9b185f987fbe88e21e9ebc9
Modified Token:
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Using the modified cookie, change the existing value of the cookie role and refresh the page.
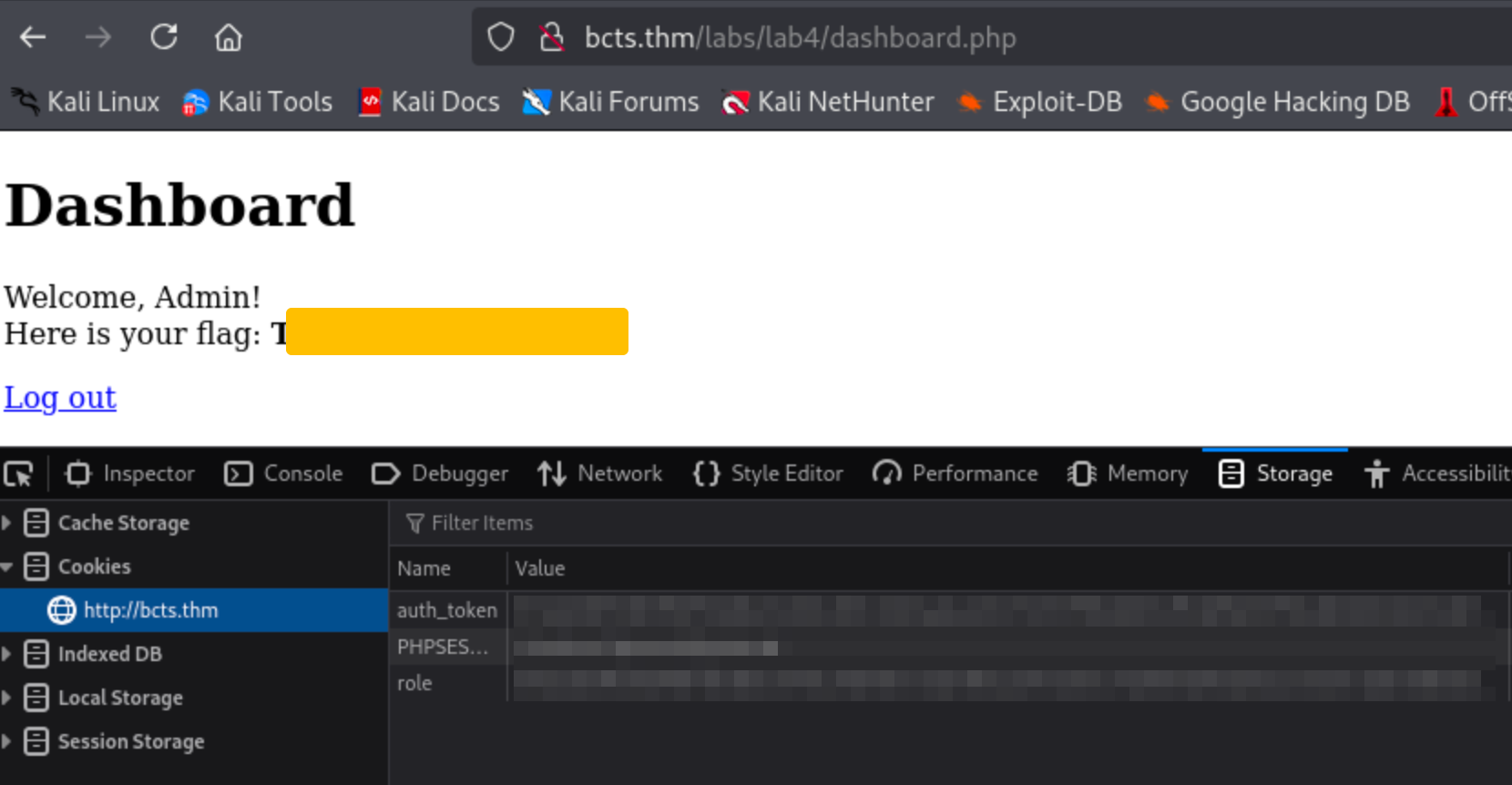
What is the flag?
Recap of Key Concepts
In this room, we’ve explored common cryptographic mistakes that developers often make, along with practical demonstrations of how these errors can be exploited. Let’s summarise the critical concepts and vulnerabilities you’ve encountered:
- Brute-forcing Keys:
- Weak or predictable keys, such as those derived from timestamps or short alphanumeric strings, can be cracked using brute-force attacks with tools like Hashcat or John the Ripper.
- Breaking Hashes:
- Outdated hash functions like MD5 and SHA-1 are vulnerable to attacks such as collision and preimage attacks.
- Lack of salting enables attackers to use rainbow tables to reverse hashes into plaintext.
- Keys Exposed in Client-Side Code:
- Hardcoding encryption keys or API secrets in front-end code exposes them to anyone with access to the application.
- This allows attackers to decrypt sensitive data or impersonate users.
- Bit Flipping Attacks:
- Unauthenticated encryption (e.g., AES-CBC without a MAC) enables attackers to modify ciphertext, resulting in controlled changes to decrypted plaintext.
Best Practices for Avoiding Cryptographic Mistakes
To secure cryptographic implementations and prevent the vulnerabilities explored in this room, follow these best practices:
- Use Strong Keys and Secure Algorithms
- Generate keys with sufficient entropy and length (e.g., AES-256 for symmetric encryption).
- Use modern, secure algorithms such as AES-GCM, RSA-2048, and SHA-256.
- Regularly update cryptographic libraries to protect against newly discovered vulnerabilities.
- Avoid Exposing Keys in Client-Side Code
- Never hardcode encryption keys, API secrets, or sensitive credentials in JavaScript or other client-side files.
- Store secrets securely on the server side and use environment variables or key management systems like AWS KMS or Azure Key Vault.
- Implement Authenticated Encryption
- Always pair encryption with integrity checks using authenticated encryption modes like AES-GCM or AES-CCM.
- Ensure that any data transmitted over untrusted channels is encrypted and includes integrity protection.
- Secure RSA Implementations
- Use larger public exponents (
e = 65537) and ensure that encrypted messages include padding (e.g., OAEP or PKCS#1). - Avoid encrypting the same plaintext for multiple recipients with the same public exponent.
- Use larger public exponents (
- Educate Developers
- Ensure that development teams understand secure cryptographic practices and the risks of misconfigurations.
- Conduct regular training and code reviews to identify and fix potential issues before deployment.
Click me to proceed to the next task.
Ready to learn Cyber Security? Create your free account today!
TryHackMe provides free online cyber security training to secure jobs & upskill through a fun, interactive learning environment.
Already have an account? Log in

