Data Representation

Our First Eight Colors

By combining different amounts of red, green, and blue lights, you can get any color you like. In computer colors, think of it like three knobs, and each knob controls one of the three colors.

Example

Let’s say that each of the three colors can be either on or off, i.e., each has two states.

• The red light can be either on or off
• The green light can be either on or off
• The blue light can be either on or off

These states give us 2 × 2 × 2 = 8, that’s eight different colors.

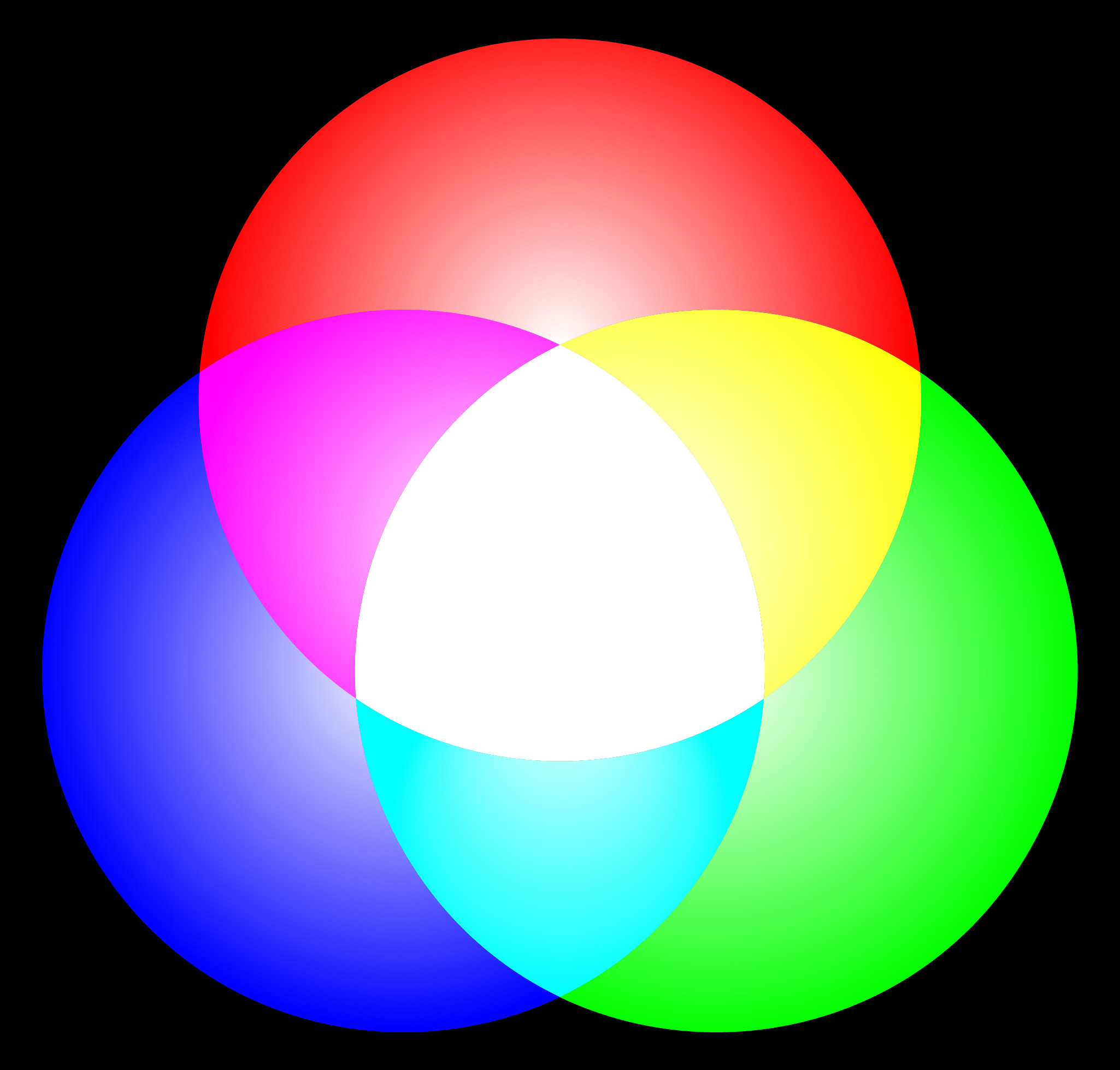
If a computer were limited to 8 colors, it would only need to indicate which color is “switched on” and which is “switched off.” In fact, it can use three digits of 1 and 0 to represent the states of red, green, and blue. For example, 111 would be all 3 lights switched on, while 100 would be only the red switched on. This digit, which can be either 1 or 0, is called a bit.

Now, a computer can represent any of the 8 colors. If this is still unclear, a detailed list is shown in the table below.

Color Representation	Representation Meaning	Color Name
000	All colors are off	Black
001	Only blue is on	Blue
010	Only green is on	Green
100	Only red is on	Red
011	Green and blue are on	Cyan
101	Red and blue are on	Magenta
110	Red and green are on	Yellow
111	All colors are on	White

We just provided a way to represent a color in a palette of 8 colors.

From 8 to 16,000,000

Being limited to eight colors is inconvenient, as we prefer millions of colors. It would be convenient if each of the 3 lights (red, green, and blue) had 256 levels instead of just 2 (on or off). Let’s repeat the same math as earlier: 256 × 256 × 256 = 16,777,216. That’s more than 16 million colors; that covers most of our needs.

One bit is enough to represent 2 states: on and off. We need 8 bits to express 256 states. In most textbooks, a group of 8 bits is referred to as a byte; however, you can also use the term octet.

Putting all this together, you would realise that a color is now represented as 3 × 8 bits, or 3 bytes (24 bits). For example, one green color used on this page is represented as 10100011 11101010 00101010; that’s not a very convenient way to type or read color codes. Here comes the hexadecimal representation to the rescue!

Hexadecimal Representation

Hexadecimal representation makes it easy to combine 4 bits into a single character, a hexadecimal digit, to be specific. For now, please think of the hexadecimal digits as symbols where each symbol represents a set of 4 bits. We will revisit hexadecimal numbers in Task 3.

Hexadecimal Digit	Binary Representation
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

Going back to the green color, instead of typing 10100011 11101010 00101010, we can type A3EA2A. In fact, that’s how you specify the color in graphics programs. For your convenience, the attached static site helps you convert a hex color into its binary and decimal representations, along with a color preview.

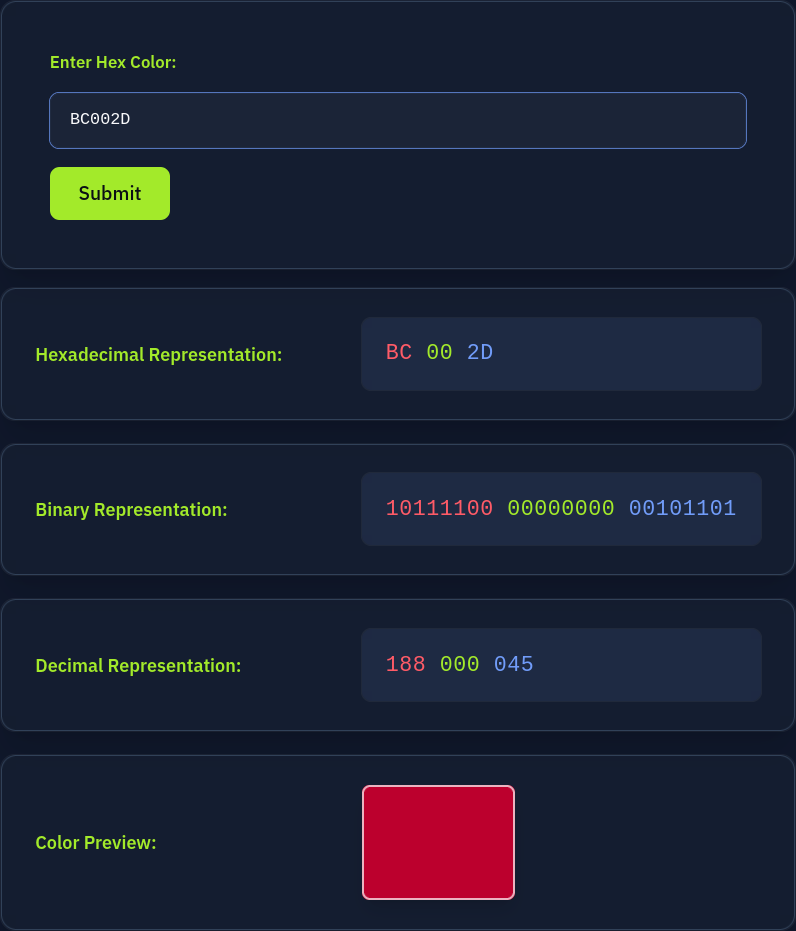
To summarise what we have covered so far:

• In real-life applications, a color is represented in 24 bits, i.e., 3 bytes
• Each byte can represent 256 different values
• Each of the three bytes specifies the intensity of the red, green, and blue lights
• Every 4 bits are represented by one hexadecimal digit
• Each byte is represented as two hexadecimal digits

Click on the View Site button below and use it to answer the following questions.

Human beings have ten fingers, and this is the most plausible explanation for why we use the decimal (base-10) system in our everyday lives. Computers, on the other hand, have two fingers states that they understand:

• Low and High in voltage range (example: transistor-transistor logic)
• North and South in magnetic polarity (example: hard disk drives)
• Light presence (example: fiber optics)

Let’s consider the first example. On the electronic level, a transistor either passes or blocks electric current. Consequently, in all digital systems, everything boils down to a low or high state, representing 0 and 1, respectively. (For example, the low range can be voltage between 0 and 0.8 volts, while the high range is between 2 and 3.3 volts, or 2.7 and 5 volts, depending on the electronic system.) We are not affected by how the 0 and the 1 are represented on the physical level; however, we are concerned with how to use these two digits to represent data, such as numbers.

In the previous task, we saw that we can use a set of bits to fine-tune the steps. For instance, 1 bit can represent 2 states, while 8 bits can represent 256 states. In this task, we will learn a bit more about the math behind it; however, don’t worry if it appears complex at first glance. Things will make more sense as you progress in your learning journey.

In simple math terms, a number such as 213 is actually the same as saying 200 + 10 + 3. Isn’t this right?

In a more technical representation, 213 can be written as 213 = 2 × 10² + 1 × 10¹ + 3 × 10⁰. As you would remember from the math class, 10² = 100, 10¹ = 10, and 10⁰ = 1.

Consequently, this was just the formal mathematical way of saying 213 = 2 × 100 + 1 × 10 + 3 × 1. If you have not worked with math for some time, please give this some thought and a second read before you move on.

Binary Numbers

The binary (base-2) system can be expressed similarly to what we wrote earlier, discussing the decimal (base-10) system. The key differences are that the binary system is limited to two digits, 0 and 1, and that everything is a power of 2. Let’s consider a couple of examples.

The binary number 1001 can be expressed as follows: 1001 = 1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰ = 1 × 8 + 0 × 4 + 0 × 2 + 1 × 1 = 8 + 0 + 0 + 1 = 9. We just demonstrated how to write 9 in binary.

Following the same approach, it won’t be challenging to convert the binary numbers 0000, 0001, 0010, 0011 to the decimal system. Let’s go through these four conversions.

0000 = 0 × 2³ + 0 × 2² + 0 × 2¹ + 0 × 2⁰ = 0 × 8 + 0 × 4 + 0 × 2 + 0 × 1 = 0

0001 = 0 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰ = 0 × 8 + 0 × 4 + 0 × 2 + 1 × 1 = 1

0010 = 0 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰ = 0 × 8 + 0 × 4 + 1 × 2 + 0 × 1 = 2

0011 = 0 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰ = 0 × 8 + 0 × 4 + 1 × 2 + 1 × 1 = 3

If this is your first time working with different bases, you might have already figured out that the rightmost digit is multiplied by 2⁰ in the case of the binary (base-2) system and multiplied by 10⁰ in the case of the decimal (base-10) system. Then, the next digit is multiplied by 2¹ in the base-2 system and by 10¹ in the base-10 system. And so forth till we reach the leftmost digit. It is easy, but requires careful attention not to miss any digit or misjudge its power.

As an exercise, we will convert four more binary numbers, 1100, 1101, 1110, and 1111, to the decimal system. Try to do this on a piece of paper before comparing your answers with the solutions below.

1100 = 1 × 2³ + 1 × 2² + 0 × 2¹ + 0 × 2⁰ = 1 × 8 + 1 × 4 + 0 × 2 + 0 × 1 = 8 + 4 + 0 + 0 = 12

1101 = 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 1 × 8 + 1 × 4 + 0 × 2 + 1 × 1 = 8 + 4 + 0 + 1 = 13

1110 = 1 × 2³ + 1 × 2² + 1 × 2¹ + 0 × 2⁰ = 1 × 8 + 1 × 4 + 1 × 2 + 0 × 1 = 8 + 4 + 2 + 0 = 14

1111 = 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰ = 1 × 8 + 1 × 4 + 1 × 2 + 1 × 1 = 8 + 4 + 2 + 1 = 15

Having come this far, it is time to revisit the hexadecimal system.

Hexadecimal Numbers

In Task 2, we grouped every 4 bits into a single hexadecimal digit. As we’ve seen earlier, a hexadecimal digit ranges between 0 and F. By taking a closer look at the table below, you will notice that a hexadecimal digit ranges between 0 and 15 in the decimal system. To replace 10, 11, 12, 13, 14, and 15 each with a single letter/digit, A, B, C, D, E, and F are chosen. The table below is something you would encounter in any tutorial or chapter on the hexadecimal system.

Decimal Number	Hexadecimal Digit	Binary Representation
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Optional: Converting From Hexadecimal to Decimal System

This subsection is optional. If you are curious about converting a hexadecimal number to a decimal number, you would follow the same approach we used for binary conversion. Let’s say that we want to convert the hexadecimal number 9B DF to decimal.

9BDF = 9 × 16³ + 11 × 16² + 13 × 16¹ + 15 × 16⁰ = 9 × 4096 + 11 × 256 + 13 × 16 + 15 × 1 = 39,903

Optional: Octal Numbers

The octal system refers to base 8. In other words, it uses the digits between 0 and 7. While the hexadecimal system uses base 16 and groups 4 bits, the octal system uses base 8 and groups 3 bits. The table below shows how the octal digits relate to their binary counterparts.

Decimal Number	Octal Digit	Binary Representation
0	0	000
1	1	001
2	2	010
3	3	011
4	4	100
5	5	101
6	6	110
7	7	111

Optional: Converting From Octal to Decimal System

Converting an octal number to its decimal equivalent follows the steps of the previous conversions. Consider the octal number 357.

357 = 3 × 8² + 5 × 8¹ + 7 × 8⁰ = 3 × 64 + 5 × 8 + 7 × 1 = 239

Click on the View Site button below and use it to answer the following questions.

In this room, we covered several topics related to how numeric values are represented and stored in computer memory. We covered the following systems:

• Decimal (Base-10) system: This is the system we use in our everyday life.
• Binary (Base-2) system: Computers understand two states, which are encoded as 0 and 1.
• Hexadecimal (Base-16) system: Every 4 binary digits (bits) can be grouped as one hexadecimal digit. A hexadecimal digit ranges between 0 and F.
• Octal (Base-8) system: Every 3 binary digits (bits) can be grouped as one octal digit. An octal digit ranges between 0 and 7. This one is less commonly encountered on computer systems.

Moreover, we learned how a color can be represented. We covered:

• Bit: It is short for binary digit, and it can be either 0 or 1.
• Byte: On modern systems, a byte is 8 bits. It is also referred to as an octet.
• Hex color: A color is represented as a combination of red, green, and blue on computer systems. If one byte is assigned for each of the primary colors (red, green, and blue), we can get more than 16 million color combinations.

In the Data Encoding room, we will explore how the alphabets of the various languages are saved. In addition to letters, we will see how emojis are saved as bits.